[Epistemic status: I have no formal training in machine learning or statistics so some of this might be wrong/misleading, but I’ve tried my best.]
Background:
Conventional wisdom says that deep neural networks are really good at learning from high dimensional data like images or spoken language, but only when they have huge amounts of labelled examples to train on. Humans on the other hand, are capable of one-shot learning - if you take a human who’s never seen a spatula before, and show them a single picture of a spatula, they will probably be able to distinguish spatulas from other kitchen utensils with astoundingly high precision.

..Yet another one of the things humans can do that seemed trivial to us right up until we tried to make an algorithm do it.
This ability to rapidly learn from very little data seems like it’s obviously desirable for machine learning systems to have because collecting and labelling data is expensive. I also think this is an important step on the long road towards general intelligence.
Recently there have been many interesting papers about one-shot learning with neural nets and they’ve gotten some good results. This is a new area that really excites me, so I wanted to make a gentle introduction to make it more accessible to fellow newcomers to deep learning.
In this post, I want to:
- Introduce and formulate the problem of one-shot learning
- Describe benchmarks for one-shot classification and give a baseline for performance
- Give an example of deep one-shot learning by partially reimplementing the model in this paper with keras.
- Hopefully point out some small insights that aren’t obvious to everyone
Formulating the Problem - N-way One-Shot Learning
Before we try to solve any problem, we should first precisely state what the problem actually is, so here is the problem of one-shot classification expressed symbolically:
Our model is given a tiny labelled training set \( S \), which has N examples, each vectors of the same dimension with a distinct label \(y\).
\[ S = \{ (x_1,y_1), …, (x_N,y_N) \} \]
It is also given \( \hat{x} \), the test example it has to classify. Since exactly one example in the support set has the right class, the aim is to correctly predict which \( y \in S \) is the same as \(\hat{x} \) ‘s label, \(\hat{y}\).
There are fancier ways of defining the problem, but this one is ours. Here are some things to make note of:
-
Real world problems might not always have the constraint that exactly one image has the correct class
-
It’s easy to generalize this to k-shot learning by having there be k examples for each \(y_i\) rather than just one.
-
When N is higher, there are more possible classes that \( \hat{x} \) can belong to, so it’s harder to predict the correct one.
-
Random guessing will average \( \frac{100}{n} \% \) accuracy.
Here are some examples of one-shot learning tasks on the Omniglot dataset, which I’ll describe in the next section.

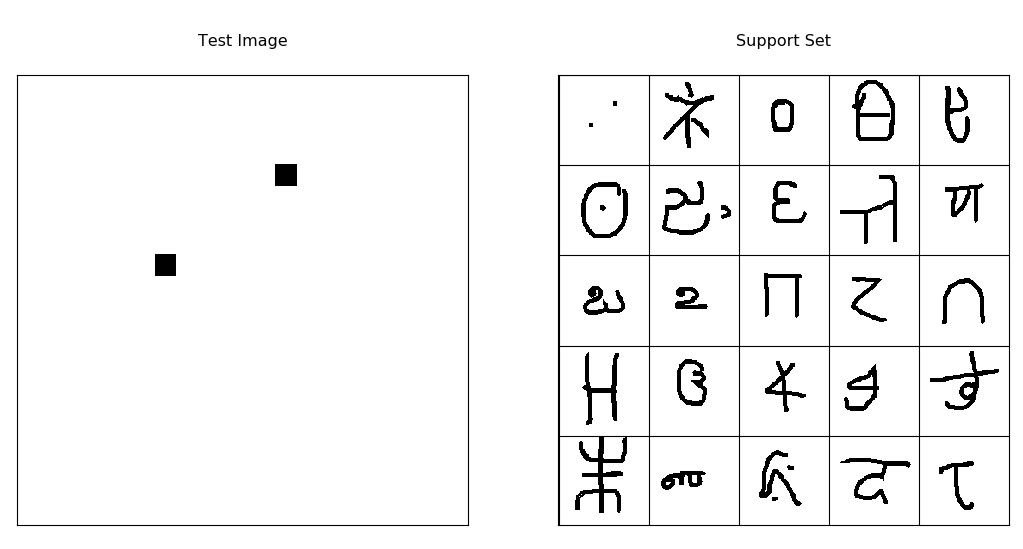

About the data - Omniglot! :
The Omniglot dataset is a collection of 1623 hand drawn characters from 50 alphabets. For every character there are just 20 examples, each drawn by a different person at resolution 105x105.
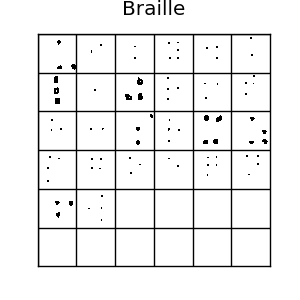
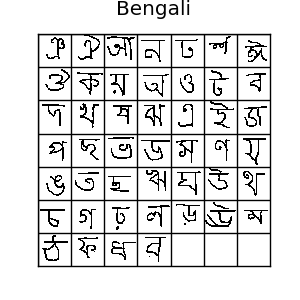
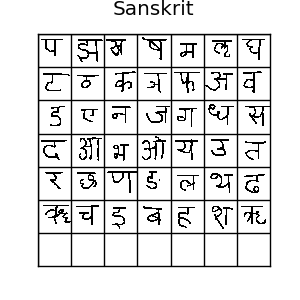
If you like machine learning, you’ve probably heard of the MNIST dataset. Omniglot is sometimes referred to as the transpose of mnist, since it has 1623 types of character with only 20 examples each, in contrast to MNIST having thousands of examples for only 10 digits. There is also data about the strokes used to create each character, but we won’t be using that. Usually, it’s split into 30 training alphabets and 20 evaluation alphabets. All those different characters make for lots of possible one-shot tasks, so it’s a really good benchmark for one-shot learning algorithms.
A One-Shot Learning Baseline / 1 Nearest Neighbour
The simplest way of doing classification is with k-nearest neighbours, but since there is only one example per class we have to do 1 nearest neighbour. This is very simple, just calculate the Euclidean distance of the test example from each training example and pick the closest one:
\[ C(\hat{x}) = \underset{c \in S}{\operatorname{argmin}} || \hat{x} - x_c || \]
According to Koch et al, 1-nn gets ~28% accuracy in 20 way one shot classification on omniglot. 28% doesn’t sound great, but it’s nearly six times more accurate than random guessing(5%). This is a good baseline or “sanity check” to compare future one-shot algorithms with.
Hierarchical Bayesian Program Learning from Lake et al gets 95.2% - very impressive! The ~30% of this paper which I understood was very interesting. Comparing it with deep learning results that train on raw pixels is kind of “apples and oranges” though, because:
- HBPL used data about the strokes, not just the raw pixels
- HBPL on omniglot involved learning a generative model for strokes. The algorithm requires data with more complicated annotation, so unlike deep learning it can’t easily be tweaked to one-shot learn from raw pixels of dogs/trucks/brain scans/spatulas and other objects that aren’t made up of brushstrokes.
Lake et al also says that humans get 95.5% accuracy in 20 way classification on omniglot, only beating HBPL by a tiny margin. In the spirit of nullius in verba, I tried testing myself on the 20 way tasks and managed to average 97.2%. I wasn’t always doing true one-shot learning though - I saw several symbols I recognised, since I’m familiar with the greek alphabet, hiragana and katakana. I removed those alphabets and tried again but still managed 96.7%. My hypothesis is that having to read my own terrible handwriting has endowed me with superhuman symbol recognition ability.
Ways to use deep networks for one shot learning?!
If we naively train a neural network on a one-shot as a vanilla cross-entropy-loss softmax classifier, it will severely overfit. Heck, even if it was a hundred shot learning a modern neural net would still probably overfit. Big neural networks have millions of parameters to adjust to their data and so they can learn a huge space of possible functions. (More formally, they have a high VC dimension, which is part of why they do so well at learning from complex data with high dimensionality.) Unfortunately this strength also appears to be their undoing for one-shot learning. When there are millions of parameters to gradient descend upon, and a staggeringly huge number of possible mappings that can be learned, how can we make a network learn one that generalizes when there’s just a single example to learn from?
It’s easier for humans to one-shot learn the concept of a spatula or the letter \( \Theta \) because they have spent a lifetime observing and learning from similar objects. It’s not really fair to compare the performance of a human who’s spent a lifetime having to classify objects and symbols with that of a randomly initialized neural net, which imposes a very weak prior about the structure of the mapping to be learned from the data. This is why most of the one-shot learning papers I’ve seen take the approach of knowledge transfer from other tasks.
Neural nets are really good at extracting useful features from structurally complex/high dimensional data, such as images. If a neural network is given training data that is similar to (but not the same as) that in the one-shot task, it might be able to learn useful features which can be used in a simple learning algorithm that doesn’t require adjusting these parameters. It still counts as one-shot learning as long as the training examples are of different classes to the examples used for one-shot testing.
(NOTE: Here a feature means a “transformation of the data that is useful for learning”.)
So now an interesting problem is how do we get a neural network to learn the features? The most obvious way of doing this (if there’s labelled data) is just vanilla transfer learning - train a softmax classifier on the training set, then fine-tune the weights of the last layer on the support set of the one-shot task. In practice, neural net classifiers don’t work too well for data like omniglot where there are few examples per class, and even fine tuning only the weights in the last layer is enough to overfit the support set. Still works quite a lot better than L2 distance nearest neighbour though! (See Matching Networks for One Shot learning for a comparison table of various deep one-shot learning methods and their accuracy.)
There’s a better way of doing it though! Remember 1 nearest neighbour? This simple, non-parametric one-shot learner just classifies the test example with the same class of whatever support example is the closest in L2 distance. This works ok, but L2 Distance suffers from the ominous sounding curse of dimensionality and so won’t work well for data with thousands of dimensions like omniglot. Also, if you have two nearly identical images and move one over a few pixels to the right the L2 distance can go from being almost zero to being really high. L2 distance is a metric that is just woefully inadequate for this task. Deep learning to the rescue? We can use a deep convolutional network to learn some kind of similarity function that a non-parametric classifer like nearest neighbor can use.
Siamese networks

This wonderful paper is what I will be implementing in this tutorial. Koch et al’s approach to getting a neural net to do one-shot classification is to give it two images and train it to guess whether they have the same category. Then when doing a one-shot classification task described above, the network can compare the test image to each image in the support set, and pick which one it thinks is most likely to be of the same category. So we want a neural net architecture that takes two images as input and outputs the probability they share the same class.
Say \( x_1 \) and \( x_2 \) are two images in our dataset, and let \( x_1 \circ x_2 \) mean “\( x_1 \) and \( x_2 \) are images with the same class”. Note that \( x_1 \circ x_2 \) is the same as \( x_2 \circ x_1 \) - this means that if we reverse the order of the inputs to the neural network, the output should be the same - \( p(x_1 \circ x_2) \) should equal \( p(x_2 \circ x_1) \). This property is called symmetry and siamese nets are designed around having it.
Symmetry is important because it’s required for learning a distance metric - the distance from \(x_1\) to \(x_2\) should equal the distance \(x_2\) to \(x_1\).
If we just concatenate two examples together and use them as a single input to a neural net, each example will be matrix multiplied(or convolved) with a different set of weights, which breaks symmetry. Sure it’s possible it will eventually manage to learn the exact same weights for each input, but it would be much easier to learn a single set of weights applied to both inputs. So we could propagate both inputs through identical twin neural nets with shared parameters, then use the absolute difference as the input to a linear classifier - this is essentially what a siamese net is. Two identical twins, joined at the head, hence the name.
Network architecture
Unfortunately, properly explaining how and why a convolutional neural net work would make this post twice as long. If you want to understand convnets work, I suggest checking out cs231n and then colah. For any non-dl people who are reading this, the best summary I can give of a CNN is this: An image is a 3D array of pixels. A convolutional layer is where you have a neuron connected to a tiny subgrid of pixels or neurons, and use copies of that neuron across all parts of the image/block to make another 3d array of neuron activations. A max pooling layer makes a block of activations spatially smaller. Lots of these stacked on top of one another can be trained with gradient descent and are really good at learning from images.
I’m going to describe the architecture pretty briefly because it’s not the important part of the paper. Koch et al uses a convolutional siamese network to classify pairs of omniglot images, so the twin networks are both convolutional neural nets(CNNs). The twins each have the following architecture: convolution with 64 10x10 filters, relu -> max pool -> convolution with 128 7x7 filters, relu -> max pool -> convolution with 128 4x4 filters, relu -> max pool -> convolution with 256 4x4 filters. The twin networks reduce their inputs down to smaller and smaller 3d tensors, finally their is a fully connected layer with 4096 units. The absolute difference between the two vectors is used as input to a linear classifier. All up, the network has 38,951,745 parameters - 96% of which belong to the fully connected layer. This is quite a lot, so the network has high capacity to overfit, but as I show below, pairwse training means the dataset size is huge so this won’t be a problem.
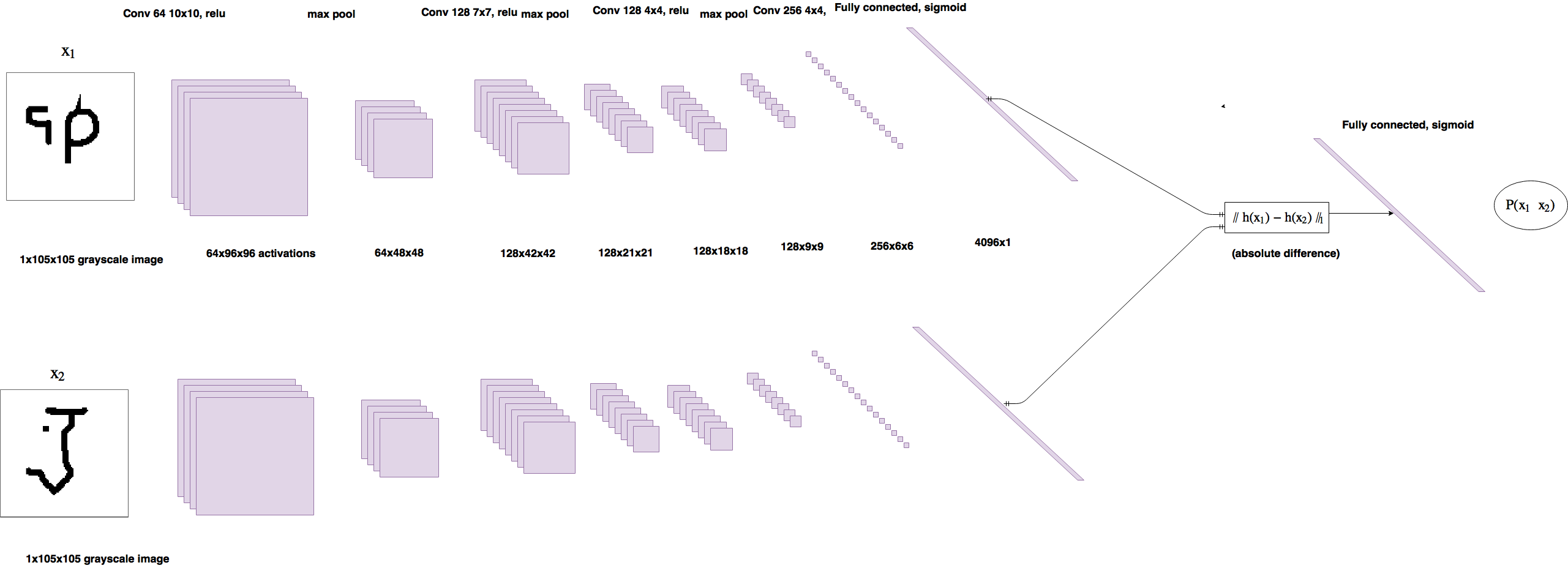
The output is squashed into [0,1] with a sigmoid function to make it a probability. We use the target \(t = 1\) when the images have the same class and \(t = 0\) for a different class. It’s trained with logistic regression. This means the loss function should be binary cross entropy between the predictions and targets. There is also a L2 weight decay term in the loss to encourage the network to learn smaller/less noisy weights and possibly improve generalization:
\[ L(x_1,x_2,t) = t \cdot log(p(x_1 \circ x_2)) + (1 - t) \cdot log(1-p(x_1 \circ x_2)) + \lambda \cdot ||w||_2 \]
When it does a one-shot task, the siamese net simply classifies the test image as whatever image in the support set it thinks is most similar to the test image: \[ C(\hat{x},S) = \underset{c}{\operatorname{argmax}} P(\hat{x} \circ x_c), x_c \in S \]
This uses an argmax unlike nearest neighbour which uses an argmin, because a metric like L2 is higher the more “different” the examples are, but this models outputs \( p(x_1 \circ x_2) \), so we want the highest. This approach has one flaw that’s obvious to me: for any \(x_a\) in the support set,the probability \( \hat{x} \circ x_a \) is independent of every other example in the support set! This means the probabilities won’t sum to 1, ignores important information, namely that the test image will be the same type as exactly one \(x \in S\)…
Observation: effective dataset size in pairwise training
EDIT: After discussing this with a PhD student at UoA, I think this bit might be overstated or even just wrong. Emperically, my implementation did overfit, even though it wasn’t trained for enough iterations to sample every possible pair, which kind of contradicts this section. I’m leaving it up in the spirit of being wrong loudly.
One cool thing I noticed about training on pairs is that there are quadratically many possible pairs of images to train the model on, making it hard to overfit. Say we have \( C\) examples each of \( E \) classes. Since there are \( C \cdot E \) images total, the total number of possible pairs is given by \[ N_{pairs} = {\binom {C \cdot E}{2}} = {\frac {(C \cdot E) !}{2! (C \cdot E-2) !}} \]
For omniglot with its 20 examples of 964 training classes, this leads to 185,849,560 possible pairs, which is huge! However, the siamese network needs examples of both same and different class pairs. There are \( E\) examples per class, so there will be \( {\binom {E}{2}} \) pairs for every class, which means there are \(N_{same} = {\binom {E}{2}} \cdot C \) possible pairs with the same class - 183,160 pairs for omniglot. Even though 183,160 example pairs is plenty, it’s only a thousandth of the possible pairs, and the number of same-class pairs increases quadratically with E but only linearly with C. This is important because the siamese network should be given a 1:1 ratio of same-class and different-class pairs to train on - perhaps it implies that pairwise training is easier on datasets with lots of examples per class.
The Code:
Prefer to just play with a jupyter notebook? I got you fam
Here is the model definition, it should be pretty easy to follow if you’ve seen keras before. I only define the twin network’s architecture once as a Sequential() model and then call it with respect to each of two input layers, this way the same parameters are used for both inputs. Then merge them together with absolute distance and add an output layer, and compile the model with binary cross entropy loss.
from keras.layers import Input, Conv2D, Lambda, merge, Dense, Flatten,MaxPooling2D
from keras.models import Model, Sequential
from keras.regularizers import l2
from keras import backend as K
from keras.optimizers import SGD,Adam
from keras.losses import binary_crossentropy
import numpy.random as rng
import numpy as np
import os
import dill as pickle
import matplotlib.pyplot as plt
from sklearn.utils import shuffle
def W_init(shape,name=None):
"""Initialize weights as in paper"""
values = rng.normal(loc=0,scale=1e-2,size=shape)
return K.variable(values,name=name)
#//TODO: figure out how to initialize layer biases in keras.
def b_init(shape,name=None):
"""Initialize bias as in paper"""
values=rng.normal(loc=0.5,scale=1e-2,size=shape)
return K.variable(values,name=name)
input_shape = (105, 105, 1)
left_input = Input(input_shape)
right_input = Input(input_shape)
#build convnet to use in each siamese 'leg'
convnet = Sequential()
convnet.add(Conv2D(64,(10,10),activation='relu',input_shape=input_shape,
kernel_initializer=W_init,kernel_regularizer=l2(2e-4)))
convnet.add(MaxPooling2D())
convnet.add(Conv2D(128,(7,7),activation='relu',
kernel_regularizer=l2(2e-4),kernel_initializer=W_init,bias_initializer=b_init))
convnet.add(MaxPooling2D())
convnet.add(Conv2D(128,(4,4),activation='relu',kernel_initializer=W_init,kernel_regularizer=l2(2e-4),bias_initializer=b_init))
convnet.add(MaxPooling2D())
convnet.add(Conv2D(256,(4,4),activation='relu',kernel_initializer=W_init,kernel_regularizer=l2(2e-4),bias_initializer=b_init))
convnet.add(Flatten())
convnet.add(Dense(4096,activation="sigmoid",kernel_regularizer=l2(1e-3),kernel_initializer=W_init,bias_initializer=b_init))
#encode each of the two inputs into a vector with the convnet
encoded_l = convnet(left_input)
encoded_r = convnet(right_input)
#merge two encoded inputs with the l1 distance between them
L1_distance = lambda x: K.abs(x[0]-x[1])
both = merge([encoded_l,encoded_r], mode = L1_distance, output_shape=lambda x: x[0])
prediction = Dense(1,activation='sigmoid',bias_initializer=b_init)(both)
siamese_net = Model(input=[left_input,right_input],output=prediction)
#optimizer = SGD(0.0004,momentum=0.6,nesterov=True,decay=0.0003)
optimizer = Adam(0.00006)
#//TODO: get layerwise learning rates and momentum annealing scheme described in paperworking
siamese_net.compile(loss="binary_crossentropy",optimizer=optimizer)
siamese_net.count_params()The original paper used layerwise learning rates and momentum - I skipped this because it; was kind of messy to implement in keras and the hyperparameters aren’t the interesting part of the paper. Koch et al adds examples to the dataset by distorting the images and runs experiments with a fixed training set of up to 150,000 pairs. Since that won’t fit in my computers memory, I decided to just randomly sample pairs. Loading image pairs was probably the hardest part of this to implement. Since there were 20 examples for every class, I reshaped the data into N_classes x 20 x 105 x 105 arrays, to make it easier to index by category.
class Siamese_Loader:
"""For loading batches and testing tasks to a siamese net"""
def __init__(self,Xtrain,Xval):
self.Xval = Xval
self.Xtrain = Xtrain
self.n_classes,self.n_examples,self.w,self.h = Xtrain.shape
self.n_val,self.n_ex_val,_,_ = Xval.shape
def get_batch(self,n):
"""Create batch of n pairs, half same class, half different class"""
categories = rng.choice(self.n_classes,size=(n,),replace=False)
pairs=[np.zeros((n, self.h, self.w,1)) for i in range(2)]
targets=np.zeros((n,))
targets[n//2:] = 1
for i in range(n):
category = categories[i]
idx_1 = rng.randint(0,self.n_examples)
pairs[0][i,:,:,:] = self.Xtrain[category,idx_1].reshape(self.w,self.h,1)
idx_2 = rng.randint(0,self.n_examples)
#pick images of same class for 1st half, different for 2nd
category_2 = category if i >= n//2 else (category + rng.randint(1,self.n_classes)) % self.n_classes
pairs[1][i,:,:,:] = self.Xtrain[category_2,idx_2].reshape(self.w,self.h,1)
return pairs, targets
def make_oneshot_task(self,N):
"""Create pairs of test image, support set for testing N way one-shot learning. """
categories = rng.choice(self.n_val,size=(N,),replace=False)
indices = rng.randint(0,self.n_ex_val,size=(N,))
true_category = categories[0]
ex1, ex2 = rng.choice(self.n_examples,replace=False,size=(2,))
test_image = np.asarray([self.Xval[true_category,ex1,:,:]]*N).reshape(N,self.w,self.h,1)
support_set = self.Xval[categories,indices,:,:]
support_set[0,:,:] = self.Xval[true_category,ex2]
support_set = support_set.reshape(N,self.w,self.h,1)
pairs = [test_image,support_set]
targets = np.zeros((N,))
targets[0] = 1
return pairs, targets
def test_oneshot(self,model,N,k,verbose=0):
"""Test average N way oneshot learning accuracy of a siamese neural net over k one-shot tasks"""
pass
n_correct = 0
if verbose:
print("Evaluating model on {} unique {} way one-shot learning tasks ...".format(k,N))
for i in range(k):
inputs, targets = self.make_oneshot_task(N)
probs = model.predict(inputs)
if np.argmax(probs) == 0:
n_correct+=1
percent_correct = (100.0*n_correct / k)
if verbose:
print("Got an average of {}% {} way one-shot learning accuracy".format(percent_correct,N))
return percent_correct..And now the training loop. Nothing unusual here, except for that I monitor one-shot tasks validation accuracy to test performance, rather than loss on the validation set.
evaluate_every = 7000
loss_every=300
batch_size = 32
N_way = 20
n_val = 550
siamese_net.load_weights("PATH")
best = 76.0
for i in range(900000):
(inputs,targets)=loader.get_batch(batch_size)
loss=siamese_net.train_on_batch(inputs,targets)
if i % evaluate_every == 0:
val_acc = loader.test_oneshot(siamese_net,N_way,n_val,verbose=True)
if val_acc >= best:
print("saving")
siamese_net.save('PATH')
best=val_acc
if i % loss_every == 0:
print("iteration {}, training loss: {:.2f},".format(i,loss))Results
Once the learning curve flattened out, I used the weights which got the best validation 20 way accuracy for testing. My network averaged ~83% accuracy for tasks from the evaluation set, compared to 93% in the original paper. Probably this difference is because I didn’t implement many of the performance enhancing tricks from the original paper, like layerwise learning rates/momentum, data augmentation with distortions, bayesian hyperparemeter optimization and I also probably trained for less epochs. I’m not too worried about this because this tutorial was more about introducing one-shot learning in general, than squeezing the last few % performance out of a classifier. There is no shortage of resources on that!
I was curious to see how accuracy varied over different values of “N” in N way one shot learning, so I plotted it, with comparisons to 1 nearest neighbours, random guessing and training set performance.
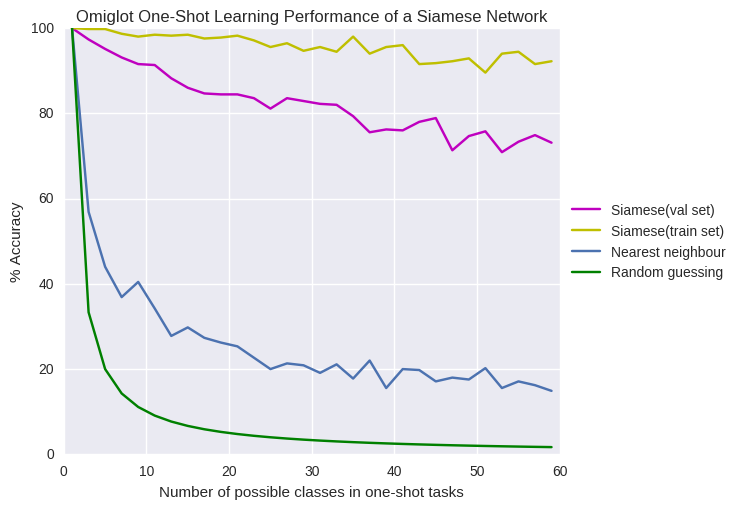
As you can see, it performs worse on tasks from the validaiton set than the train set, especially for high values of N, so there must be overfitting. It would be interesting to see how well traditional regularization methods like dropout work when the validation set is made of completely different classes to the training set. It works better than I expected for large N, still averaging above 65% accuracy for 50-60 way tasks.
Discussion
We’ve just trained a neural network trained to do same-different pairwise classification on symbols. More importantly, we’ve shown that it can then get reasonable accuracy in 20 way one-shot learning on symbols from unseen alphabets. Of course, this is not the only way to use deep networks for one-shot learning.
As I touched on earlier, I think a major flaw of this siamese approach is that it only compares the test image to every support image individualy, when it should be comparing it to the support set as a whole. When the network compares the test image to any image \(x_1\), \( p( \hat{x} \circ x_1) \) is the same no matter what else is the support set. This is silly. Say you’re doing a one-shot task and you see an image that looks similar to the test image. You should be much less confident they have the same class if there is another image in the support set that also looks similar to the test image. The training objective is different to the test objective. It might work better to have a model that can compare the test image to the support set as a whole and use the constraint that only one support image has the same class.
Matching Networks for One Shot learning does exactly that. Rather than learning a similarity function, they have a deep model learn a full nearest neighbour classifier end to end, training directly on oneshot tasks rather than on image pairs. Andrej Karpathy’s notes explain it much better than I can. Since you are learning a machine classifier, this can be seen as a kind of meta-learning. One-shot Learning with Memory-Augmented Neural Networks explores the connection between one-shot learning and meta learning and trains a memory augmented network on omniglot, though I confess I had trouble understanding this paper.
What next?
The omniglot dataset has been around since 2015, and already there are scalable ML algorithms getting within the ballpark of human level performance on certain one-shot learning tasks. Hopefully one day it will be seen as a mere “sanity check” for one-shot classification algorithms much like MNIST is for supervised learning now.
Image classification is cool but I don’t think it’s the most interesting problem in machine learning. Now that we know deep one-shot learning can work pretty good, I think it would be cool to see attempts at one-shot learning for other, more exotic tasks.
Ideas from one-shot learning could be used for more sample efficient reinforcement learning, especially for problems like OpenAI’s Universe, where there are lots of MDPs/environments that have similar visual features and dynamics. - It would be cool to have an RL agent that could efficiently explore a new environment after learning in similar MDPs.

One-shot Imitation learning is one of my favourite one-shot learning papers. The goal is to have an agent learn a robust policy for solving a task from a single human demonstration of that task.This is done by:
- Having a neural net map from the current state and a sequence of states(the human demonstration) to an action
- Training it on pairs of human demonstrations on slightly different variants of the same task, with the goal of reproducing the second demonstration based on the first.
This strikes me as a really promising path to one day having broadly applicable, learning based robots!
Bringing one-shot learning to NLP tasks is a cool idea too. Matching Networks for One-Shot learning has an attempt at one-shot language modeling, filling a missing word in a test sentence given a small set of support sentences, and it seems to work pretty well. Exciting!
Conclusion
Anyway, thanks for reading! I hope you’ve managed to one-shot learn the concept of one-shot learning :) If not, I’d love to hear feedback or answer any questions you have!
comments powered by Disqus
